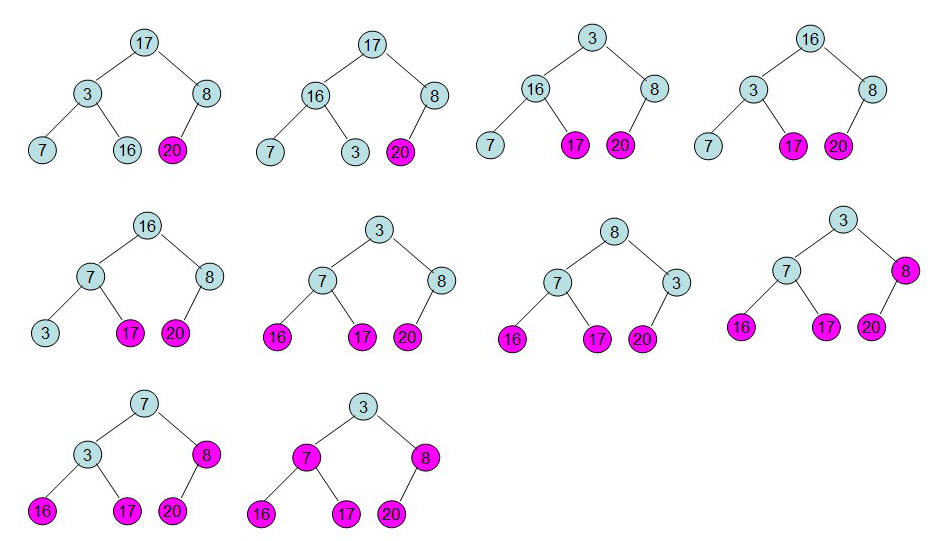
堆是在节点上存储数据的完全二叉树， 小顶堆是把对中最小值一直保持在堆顶的树型结构。其中主要通过替换父子节点来实现

• 向上筛选： 将新的值插入到堆尾，并通过与父节点(循环)比较来对换位置。
• 向下筛选： 将堆尾放入到已弹出的堆顶部，通过与子节点(循环)比较来对换位置。

class PriorityQue {
  constructor(heap = []) {
    this.heap = heap
    this.build()
  }

  getSize() {
    return this.heap.length
  }

  upward(i) {
    // 向上筛选
    // i 是数组下标, 符合条件替换父子节点
    while (this._parent(i) >= 0 && i > 0) {
      if (this.heap[this._parent(i)] > this.heap[i]) {
        let tmp = this.heap[i]
        this.heap[i] = this.heap[this._parent(i)]
        this.heap[this._parent(i)] = tmp
      }
      i = this._parent(i)
    }
  }

  downward(i) {
    // 向下筛选， 获取子节点中最小值，替换父节点
    while (i * 2 <= this.getSize()) {
      let idx = this.minChild(i)

      if (this.heap[i] > this.heap[idx]) {
        let tmp = this.heap[idx]
        this.heap[idx] = this.heap[i]
        this.heap[i] = tmp
      }
      i = idx > 0 ? idx : 1
    }
  }

  minChild(i) {
    // 如果没有右子节点， 返回左子节点
    let left_idx = i * 2
    let right_idx = i * 2 + 1
    if (right_idx > this.getSize()) {
      return left_idx
    } else if (this.heap[left_idx] < this.heap[right_idx]) {
      return left_idx
    } else {
      return right_idx
    }
  }

  _parent(i) {
    // 父节点下标
    return Math.floor(i / 2)
  }

  enqueue(e) {
    // 压入堆中
    this.heap.push(e)
    this.upward(this.getSize())
  }

  dequeue() {
    // 弹出堆顶
    let e = this.heap[0]
    this.heap[0] = this.heap[this.getSize() - 1]
    this.heap.pop()
    this.downward(0)
    return e
  }

  build() {
    let i = this.getSize()
    while (i > 0) {
      this.upward(i)
      i -= 1
    }
  }
}

let q = new PriorityQue([5, 4, 3, 2, 1])
console.log(q)
for (let i = 0; i < 5; i++) {
  q.dequeue()
}